6.1 기술통계
- 학습목표 : 통계학의 기초를 이해하고 표본의 특성을 파악하여 (데이터 요약 등) 데이터의 특징을 정리하는 기술 통계에 대해서 학습한다.
6.1.1 데이터 요약
6.1.1.1 통계학의 이해
- 통계학의 정의
- 모집단(Population) : 관심 대상 전체 (예를 들면 유권자 전체)
- 표본(Sample) : 모집단에서 추출한 부분집합
표본(일부 자료)를 수집한 후, 표본의 특성을 통해 모집단의 특성을 추론하는 학문
https://www.omniconvert.com/what-is/sample-size/ - 표본추출(Sampling) : 모집단에서 특정 수만큼 표본을 추출하는 과정
- 추론/추정(Inference) : 표본에서 모집단을 추론하는 과정 (ex. 추정, 가설 검정)
- 표본오차(Sampling Error) : 모집단의 모수와 표본의 통계량의 차이 (ex. 표본 평균값과 실제 모집단 평균과의 차이)
빅데이터의 발전은 모집단을 전수조사하는 것도 가능하게 한다. 그렇지만 오차를 감수하고 표본을 추출하여 모집단을 추론하는 이유는 표본추출이 모집단을 전수조사하는 것보다 시간과 노력(인적, 물적)을 아낄 수 있기 때문이다.
- 기술통계(Descriptive Statistics)와 추론통계(Inferential Statistics)
- 기술 통계 : 측정이나 실험에서 수집한 자료(data)의 정리, 요약, 해석, 표현 등을 통해 자료의 특성을 규명하는 통계적 방법 (출처: 위키백과)
- 추론 통계 : 관심 대상 전체 모집단으로부터 일부의 샘플을 추출, 분석하여 그 결과로부터 전체 모집단에 대한 특성을 예측/추론하는 과정
- 추론 통계를 하기 위해서는 기술 통계가 선행되어야 한다. 그 이유는 표본조사를 통해 표본집단의 특성을 나타내는 통계량(Statistics)을 구한 다음에 (기술 통계), 그것을 바탕으로 모집단의 특성. 즉 모수(Parameter)를 추론하기 때문이다(추론 통계)
- 기술 통계 : 측정이나 실험에서 수집한 자료(data)의 정리, 요약, 해석, 표현 등을 통해 자료의 특성을 규명하는 통계적 방법 (출처: 위키백과)
6.1.1.2 통계 자료(데이터) 측정의 이해
- 자료(Data)
- 변수 : 개체(item)의 속성을 측정한 값 (ex. 키)
- 척도 : 변수들의 값을 부여하는 방법
-> 변수는 대상의 속성을 척도로 측정하여 수치로 계량화하는 규칙
관심 대상의 속성을 관찰하여 변수값으로 저장하는 과정을 측정(Measure)이라 하고, 그 결과로 생성된 변수값들을 총칭하여 자료(Data)라 한다.

[그림에 대한 추가 설명]
- 변수가 여러 개인 경우, 변수 간의 관계를 밝히고자 데이터를 분석할 수 있음, 예를 들어 키와 몸무게의 관계 등.
- 통계학에서 변수의 개수는 '차원'이라고 표현하기도 함, 1변수 데이터는 직선 위에, 2변수 데이터는 2차원 평면 위 점으로 나타낼 수 있음
- 통계적 자료의 종류
- 질적자료: 수치화되지 않은 자료의 상태 (ex. 몸무게가 무겁다, 키가 크다), 범주형 자료로 표현하기도 함
- 양적자료: 질적자료를 객관적인 도구를 이용하여 측정하거나 평가하여 수치화한 자료 (ex. 몸무게 40kg, 키가 150cm이다), 연속형 자료로 표현하기도 함
- 척도(scale) 일정한 규칙을 가지고 기호 또는 숫자로 나타낸 값
※ 척도의 종류에 따라 자료(데이터)의 처리 방식이 달라진다. 범주형 자료의 평균은 의미가 없으며, 빈도수(Frequency)를 정량화해서 분석이 필요하다. 연속형 자료는 평균과 편차 등 산출이 가능하다.

6.1.1.3 단변량 자료의 요약

6.1.1.4 다변량 자료의 요약

(분석 기법에 대해서는 Chapter 8, Chapter 9에서 다룰 예정)
6.1.2 표본추출
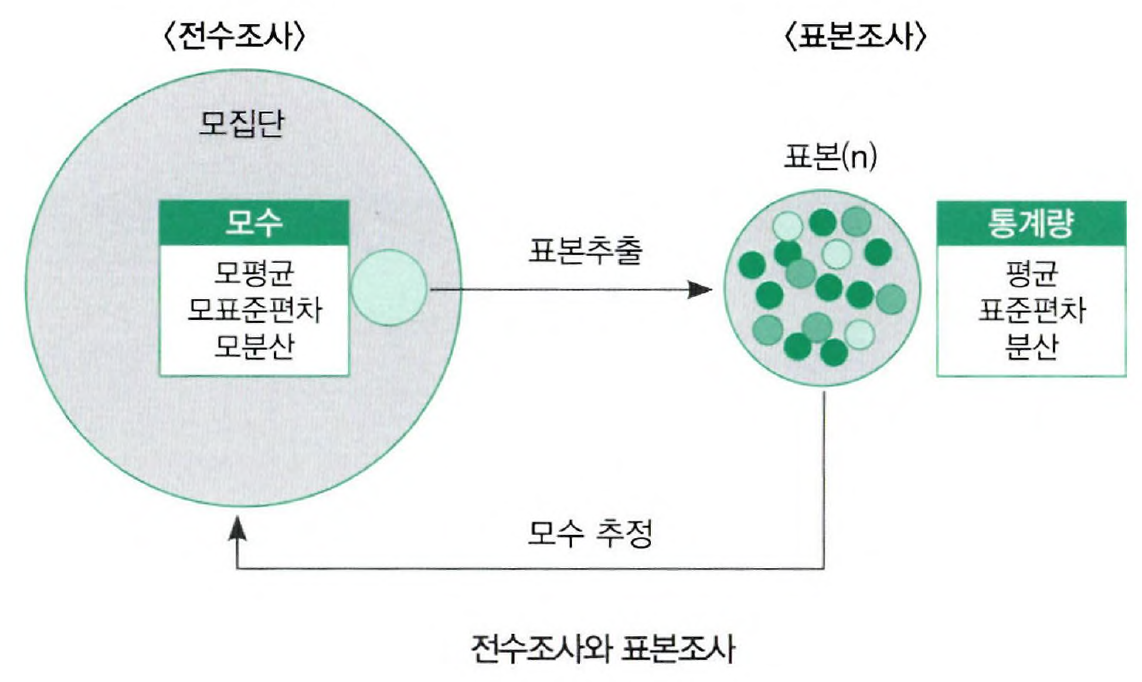
6.1.2.1 표본조사의 이해
- 전수조사: 모집단 전체를 대상으로 조사하는 방법
- 표본조사: 전체에서 일부의 부분 집단을 선택한 후, 그 일부 집단에 대해서 조사한 자료를 분석하여 전체 집단의 특성을 추정하는 방법

6.1.2.2 표본추출절차


6.1.2.3 표본추출
- 표본추출방법

- 확률표본추출법(Probability Sampling)
- 단순확률표본추출(Simple Random Sampling, 단순임의추출법 = 단순무작위추출법)
통계 조사에서 가장 기본이 되는 표본추출법이며, 모집단을 구성하는 요소 하나하나가 뽑힐 확률 이 동일한 상황(무작위 : random) 에서 뽑는 방법
- 단순확률표본추출(Simple Random Sampling, 단순임의추출법 = 단순무작위추출법)

- 계통표본추출(Systematic Sampling) * 기출
k번째 간격마다 하나씩 표본으로 추출하는 방법, 표본의 크기 n은 전체 모집단의 크기가 N인 경우에 n = N/k

- 층화확률표본추출(Stratified Random Sampling)
서로 겹치지 않는 여러 개의 층으로 분할한 후(층화 : 모집단을 몇개의 부분군으로 나누는 작업), 각 층별로 단순확률표본추출법을 적용시켜 표본을 추출

- 집락표본추출(Cluster Sampling, 군집표본추출) * 기출
서로 인접한 기본 단위들로 구성된 집락(군집)을 만들고, 추출된 집락 내의 일부 또는 전체를 조사하여 표본을 추출하는 방법

- 다단계표본추출(Multistage Sampling)
- 비확률표본추출법(Non-Probability Sampling)
- 편의표본추출(Convenience Sampling)
- 판단표본추출(Judgement Sampling, 유의추출법, 판단표집)
- 할당표본추출(Quota Sampling)
- 눈덩이표본추출(Snowball Sampling)
- 지원자표본추출(Volunteer Sampling)
6.1.2.4 표본크기와 표본오차와의 관계
일반적으로 표본수가 크면 표본오차는 작아지나, 많이 조사한다고 표본오차가 무한정 작아지진 않는다.
따라서 표본오차를 최소화하는 효율적인 표본 수의 선정이 필요하다

6.1.3 확률분포
6.1.3.1 통계학과 확률

- 확률의 정의
어떤 사건이 발생할 가능성(경우의 수)을 0과 1 사이의 숫자로 표현한 것(척도) - 시행과 사건


- 사건의 기본 연산

- 확률의 종류(수학적 확률과 통계적 확률)
- 고전적 확률(Classical Probability, 이론적 확률, 수학적 확률)
- 경험적 확률(Empirical Probability, 통계적 확률, 객관적 확률)
- 공리적 확률(Probability Defined by Axioms)
6.1.3.2 확률의 규칙
- 여사건의 확률(Complementary Event) : 어떤 시행에서 사건 A가 일어나지 않는 사건

- 확률의 덧셈법칙(Additive rule of Probability) : 어떤 시행에서 발생한 두 사건을 A와 B라 할 때, A 또는 B가 발생하는 사건의 확률

- 독립사건과 종속사건
두 사건 A, B가 존재할 때, 한 사건의 결과가 다른 사건에 영향을 주지 않으면 독립사건이라고 하며 한 사건의 결과가 다른 사건에 영향을 주면 종속사건이라고 한다.
(독립사건의 곱셈법칙과 종속사건의 곱셈법칙)
6.1.3.3 확률의 계산
- 복원추출과 비복원추출
- 복원추출 : 표본을 한 번에 하나씩 추출할 때 한 번 추출된 원소를 다음 표본추출 대상에 포함시키는 방법이다. 같은 표본이 중복해서 나올 수 있기 때문에, 표본공간이 변하지않고 독립사건이 된다.
- 비복원추출 : 한 번 추줄된 원소는 다음 표본추줄 대상에서 포함 시키지 않고 제외시키는 방법이다. 같은 표본이 중복해서 나올 수 없기 때문에, 표본공간이 바뀌게 되고. 이는 선택으로 인해 표본공간이 바뀌는 종속사건에 해당한다.

- 경우의 수(The number of case)
사건의 원소의 개수, (ex. 주사위를 던졌을 때 짝수의 눈이 나오는 경우의 수는 3개)
추출방법과 배열순서에 따른 경우의 수는 순열, 조합, 중복순열, 중복조합 이 4가지 상황으로 정리됨
- 순열 : 순서를 고려하면서 비복원추출하여 얻어진 경우의 수
- 중복순열 : 순서를 고려하면서 복원추출하여 얻어진 경우의 수
- 조합 : 순서를 고려하지 않으면서 비복원추출하여 얻어진 경우의 수(동일한 번호로 구성된 순서열은 같은 것으로 처리)
- 중복조합 : 순서를 고려하지 않으면서 복원추출하여 얻어진 경우의 수
| 경우의 수를 구하는 4가지 상황 | 사례 | 경우의 수 산출 |
| 순열 | 6곡이 들어있는 MP3 플레이어가 있을 때, 6곡을 순서대로 중복 없이 들을 수 있는 경우의 수 | (n!) = n factorial 6 x 5 x 4 x 3 x 2 x 1 = 720 |
| 중복순열 | 3개의 편지를 2개의 우체통에 넣을 수 있는 경우의 수 | 3 Π 2 = 3x3 = 9 (Π : 파이) |
| 조합 | 6곡이 들어있는 MP3 플레이어가 있다. 6곡을 순서에 상관없이, 이 중 3곡을 중복없이 들을 수 있는 경우의 수 | 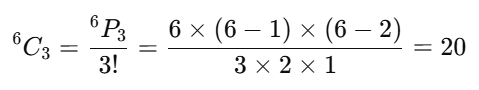 |
| 중복조합 | 어떤 꽃가게에 국화, 장미, 백합 세 종류의 꽃이 있다. 어떤 사람이 세 종류의 꽃을 선택해서 꽃 4송이를 사려고 한다. 이때 꽃 4송이의 구성은 세 종류의 꽃 중에 아무 것이라도 상관 없다고 한다. 가능한 경우의 수는? | 3종류의꽃구성 n = 3 중복 허용 r = 4  |
6.1.3.4 확률변수와 확률분포
- 확률변수와 확률분포의 이해
- 확률의 정의 : 어떤 사건이 발생할 가능성을 0과 1사이의 숫자로 표현한 것

- 확률변수 : 확률이 달라지는 변수 (ex. 위 그림에서 붉은 구슬, 흰 구슬)
- 확률함수(Probability Function. 또는 확률분포함수)는 확률변수에 의해 정의된 실수를 0과 1사이의 확
률로 대응시키는 함수를 말한다. - 확률함수를 이용해 확률변수가 발생할 확률을 알 수 있다.
- 특정 확률변수의 확률함수를 알고 있다면, 특정 사건이 일어날 확률을 예측할 수 있기 때문에 통계학에
서 큰 의미를 가진다. - 확률분포(Probability Distribution) : 가로축에 확률변수를, 세로축에 그 확률변수의 발생가능성을 표시한 분포
(책에서) 어떤 확률변수가 취할 수 있는 모든 가능한 값들에 대응하는 확률이 어떻게 분포되어 있는지를 의미하며 표본의 분포가 아닌, 모집단의 형태(확률구조)를 나타낸다.
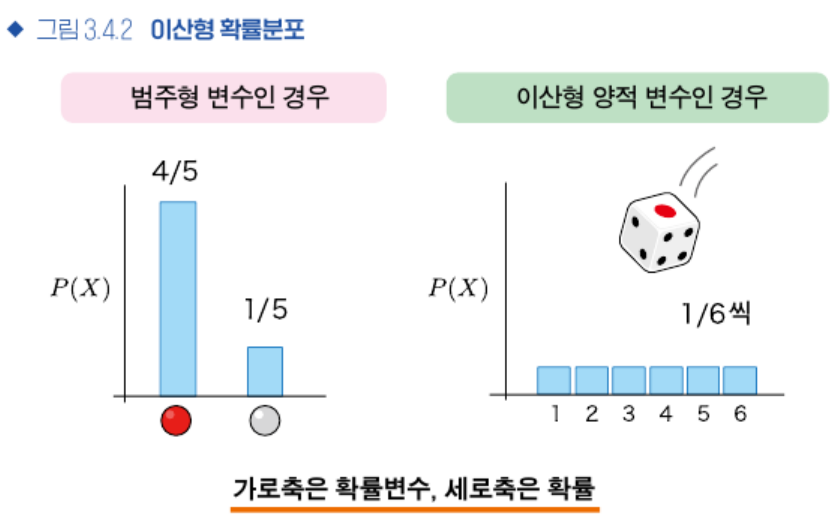
- 확률변수는 이산확률변수(Discrete Random Variable)와 연속확률변수(Continuous Random
Variable)로 나누며, 각 확률변수의 값들에 대응하는 확률의 분포를 이산확률분포와 연속확률분포로 구
분한다.
- 이산확률변수와 이산확률분포
- 확률변수 X가 셀 수 있는 특정한 수치(정수)만을 가질 때, 그 확률변수를 이산확률변수라 한다.
- 이때, 이산확률변수 X가 어떤 값 X를 가진 확률 P{X = X 를 이산확률변수 X의 확률질량함수(Probability
Mass Function, )라 한다.
- 연속확률변수와 연속확률분포
확률변수가 실수면 소수점 이하 자리가 무한히 계속될 수 있으므로, 확률변수가 하나의 값일 확률은 0이 된다. 그래서 연속형 확률변수의 경우에는 값에 일정한 범위를 두고 확률을 계산, 그 확률을 계산하는 함수를 확률밀도함수라고 한다.
확률변수가 어떤 값에서 어떤 값까지의 범위에 들어갈 확률을 알고 싶다면, 확률밀도함수를 적분하여 x축과 확률밀도함수로 둘러싸인 부분의 넓이를 구한다. 이 넓이가 바로 확률에 해당.
확률변수의 정의역 전체를 적분하면 1이 된다.

- 확률변수의 기대값과 분산
- 기댓값 : 확률변수의 가중평균, 확률변수 X가 가질 수 있는 값들과 그 값들이 발생할 확률의 곱의 합

- 분산 : 확률변수 X의 값들이 기댓값 E(X)을 기준으로 얼마나 흩어져있는지를 나타내는 값

6.1.3.5 이산확률분포의 종류

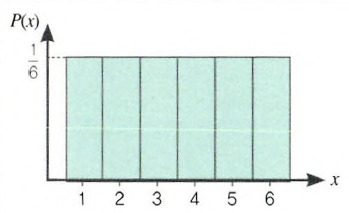
- 이산균등분포(Discrete Uniform Distribution)
확률변수 X가 n개의 이산값 {x1, x2, x3, x4...}을 가지며 각 값들이 취할 확률이 동일한 경우
ex. 주사위 1회 던지는 주사위 실험
- 베르누이분포(Bernoulli Distribution)
- 베르누이 시행(Bernoulli Trial)이란 확률 실험의 결과가 성공(Success, S)혹은 실패(Failure, F)와 같이 두 가지 결과로만 나타나는 실험
- 베르누이분포는 확률론과 통계학에서 매 시행마다 오직 두 가지의 가능한 결과만 일어난다고 할 때, 이러한 실험을 1 회 시행하여 일어난 두 가지 결과에 의해 그 값이 각각 0과 1 로 결정되는 확률분포
ex. 동전 던지기

- 이항분포(Binomial Distribution)
- ‘성공’에 해당하는 사건(사상)이 출현할 확률이 p인 똑같은 베르누이 시행을 독립적으로 n번 반복해서 시행하여 일어난 두 가지 결과에 의해 그 값이 각각 0과 1 로 결정되는 확률분포
- ex. 동전을 10번 던져서 7번 앞면이 나올 확률실험 - 초기하분포(Hypergeometric Distribution)
- 이항분포는 독립 시행. 복원추출로 실험조건이 일정하지만, 초기하분포는 비복원추출로 매 시험조건이 달라지며, 유한 모집단의 개수 N이 충분이 크면 초기하분포는 이항분포를 따른다
- 정리하면, 모집단이 N이며 구하고자 하는 대상의 수가 D인 경우, n개의 표본을 비복원으로 뽑았을 때, 구하고자 하는 수 x를 X의 확률분포로 정의한다.
- ex. 로또복권 추첨
확률변수 X는 7개의 표본 안에 내가 선택한 번호 x개가 포함될 확률 - 기하분포(Geometric Distribution)
- 베르누이 시행을 독립적으로 반복해 나가는 시행에서 확률변수 X를 첫번째 성공이 발생할 때까지 총 시행횟수라고 정의하면, 이 확률변수는 기하분포를 따른다.
- 예를 들어, 두 남녀가 연애를 하는데 일반적으로 연애를 해서 결혼할 확률은 10%라고 가정하자. 이때 확률변수 X는 x번째 사귄 이성과 결혼할 확률을 의미한다.
- 즉, 첫 번째 성공이 일어날 때까지 시행횟수를 가지고 확률분포를 설명한 것 - 음이항분포(Negative Binomial Distribution)
- 베르누이 시행을 독립적으로 반복해 나가는 시행에서 확률변수 X를 r번째 성공이 발생할 때까지 총 시행횟수라고 정의하면 이 확률변수는 음이항분포를 따른다.
- 예를 들어 어느 야구선수가 안타를 칠 확률은 25%이다. 이때 확률변수 X는 이 선수가 7(x)번째 타석에 서 3(r)번째 안타를 칠 확률을 의미한다. - 포아송분포(Poisson Distribution)
- 독립성, 비례성, 비집락성인 3가지 포아송가정을 만족하는 실험에서 크기가 1 인 단위시간 또는 단위공간 내에 평균적으로 발생하는 사건의 수를 λ (람다)라고 할 때, 확률변수 X를 단위시간 당 또는 단위공간 당 발생하는 사건의 수로 정의하면 이 확률변수는 포아송분포를 따른다.
- 어떤 단위시간이나 단위공간 내에서 사건이 몇 번 정도 일어나는지 알거나 혹은 내가 원하는 구간 동안 에 사건이 몇 번 일어나는지 알고 싶은 경우 사용하는 분포이다.
- 예를 들어, 매시간(단위시간) 접수되는 문의 요청건수(발생횟수), 한 페이지당(단위공간) 발견된 오타의 수(발생횟수) 등의 확률을 구할 때 사용할 수 있다.
6.1.3.6 연속확률분포의 종류
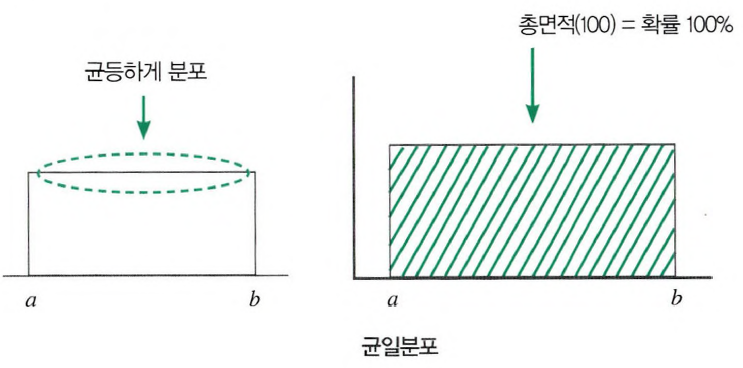
- 균등분포(Continuous Uniform Distribution)
- 임의의 실수구간 a, b에서 나타날 가능성이 동일한 확률변수를 균일확률변수라 하고 모든 확률변수에
대해 균일한 확률을 갖는 분포이다. 균일분포는 균등분포로 부르기도 한다
- 정규분포(Normal Distribution)
- 정규분포는 평균을 중심으로 좌우대칭이고 종 모양을 갖는 확률분포이며. 가우스분포(Gaussian Distribution)라고도 한다.
확률값이 가운데 있는 평균 근처에 많이 분포하고 평균에서 멀어질수록 적게 분포하기 때문에 종 모양을 갖고 있다.
- 정규분포의 모양은 평균과 분산에 의해 결정된다. (평균, 분산 = 파라미터 parameter, 모수)
- 표준편차의 크기가 커질수록 그래프의 모양은 점점 옆으로 퍼지고 반대로 작아질수록 그래프의 모양은 뾰족해지며, 평균값에 따라 좌우로 그래프가 이동하게 된다.

- 표준정규분포(Standard Normal Distribution)
- 각 집단의 평균과 표준편차가 달라 서로 비교하기 어려운 문제를 해결하기 위해 (서로 다른 모수(parameter)를 가진 정규분포를 비교하기 위해 정규분포를 평균이 0, 표준편차를 1로 표준화할 수 있음 - 이러한 과정을 거쳐 표준화된 정규분포를 표준정규분포라 한다.

- 감마분포(Gamma Distribution)
- 포아송 가정을 만족하는 실험에서, 양의 실수구간에서 정의한 어떤 사건이 a번 발생하기까지의 대기시간에 관한 확률변수를 감마확률변수라 하고 이때 확률변수 X는 감마분포를 따른다고 한다. - 지수분포(Exponential Distribution)
- 단위시간당 또는 단위공간당 발생하는 사건 수에 대한 분포는 이산확률분포인 포아송분포를 따르며, 단위시간당 평균적으로 사건이 번 발생하는 실험에서 첫 번째 사건이 발생할 때까지 걸린 시간에 대한 분포는 지수분포를 따른다. - 카이제곱분포(Chi-square Distribution)
- 카이제곱분포와 F분포는 모두 데이터가 흩어진 정도, 즉 치우침을 나타내는 분산의 특징을 확률분포로 만든 분포이며, 카이제곱분포가 한 집단의 (표본)분산을 추론하는 분포라면 月분포는 두 집단의 (표본)분산을 비교하는 분포이다.
- 카이제곱분포는 t분포와 마찬가지로 확률을 구할 때 사용하는 분포가 아니며, 추론 통계에서 신뢰구간 및 가설 검정에서 사용된다. 또한 분산이라는 제곱된 값을 다루기 때문에 (-)값은 존재하지 않고 (+)값만 존재한다. 그래서 정규분포는 x축을 중심으로 좌우대칭 모양을 표현하고 카이제곱분포는 우측 꼬리가 긴 비대칭 모양을 표현한다.
6.1.4 표본분포
6.1.4.1 통계량
확률분포는 확률변수가 특정한 값을 가질 확률을 나타내는 함수를 의미하며. 통계량(Statistic)은 어떤 확률분포로부터 관찰될 수 있는 모든 관측값들이며 , 확률표본을 구성하는 확률변수들의 함수이다. 통계량은 값이 알려져 있지 않은 모수들을 포함하지 않으며, 관측 가능한 확률변수들의 실수값 함수를 말한다. 통계량 자체는 확률변수를 말하며, 자기 자신의 확률분포를 갖게 된다.
- 표본평균(Sample Mean) : 표본의 평균
- 표본분산(Sample Variance) : 표본의 분산
- 표본표준편차(Sample Standard Deviation) : 표본분산의 양의 제곱근
- 표본비율(Sample Proportion) : 전체 중에서 사건이 차지하는 크기
6.1.4.2 표본분포
- 표본분포는 모집단에서 일정한 크기(n)로 표본을 모두 (k번) 뽑아서 계산한 각 표본 통계량의 확률분포
- 확률표본을 구성하는 확률변수들의 함수를 통계량이라고 하며(표본평균, 표본분산 등) 통계량은 관측된 표본에 따라 변하는 확률변수로 확률분포를 가지게 된다. 즉, 통계량의 확률분포를 표본분포라고 한다.
6.1.4.3 표본평균의 분포
- 표본평균의 분포(Sampling Distribution of Mean)
특정한 모집단에서 동일한 크기(n)로 표본(k번)을 뽑아서 각각의 표본들의 평균을 계산했을 때, 그 평균들의 확률분포
- 표본오차(Sampling Error) : 모집단에서 표본을 선택하여 평균 계산 시 발생하는 모집단 평균과의 차이
- 표준오차(Standard Error) : 표본평균의 표준편차
- 표본평균을 이용한 모평균 추정은 모집단의 분산(표준편차)이 알려져 있는 경우, 혹은 모집단의 분산이 알려져 있지 않고 대표본인 경우(n이 30 이상인 경우)는 중심극한의 정리에 의거하여 Z분포를 이용하고, 모집단의 분산이 알려져 있지 않고 소표본(n이 30 미만)인 경우는 t분포를 이용한다. - 중심극한정리(Central Limit Theorem)
추출한 표본의 n이 충분히 크면(일반적으로 n이 30이상이면) 모집단 분포의 모양에 상관없이 추출된 표본들의 평균의 분포는 표준정규분포 N(0,1)를 따른다는 법칙
-> 모집단이 어떤 분포를 가지는지 상관없이 표본의 크기가 충분히 크다면 표본평균들의 분포가 모집단의 모수를 기반으로 정규분포를 이룬다는 점을 이용하여 특정 사건이 일어날 확률값을 계산할 수 있음 - t분포(Student t-Distribution)
모분산(표준편차)이 알려져 있지 않고, 표본이 충분하지 못한 경우(일반적으로 n <30이면)는 정규분포보다 예측 범위가 넓은 t분포를 사용한다.
6.1.4.4 표본비율의 분포
6.1.4.5 표본분산의 분포
- 표본분산의 분포
- 모집단의 모분산을 추정하기 위한 통계량은 표본분산이다. 표본분산은 모집단이 1 개인 경우 카이제곱 분포로 통계량을 산출하고, 서로 다른 모집단을 비교할 때 F분포로 통계량을 산출한다. - F분포
- F분포는 카이제곱분포와 마찬가지로 분산을 다루는 분포이며, 카이제곱분포 2개의 비율 확률분포다. 즉, 두 집단의 산포를 비교하는데 이용한다.
- F분포는 두 집단의 분산을 나눗셈을 이용하여 비교하며. 두 정규모집단의 모분산들의 비(Ratio)에 대한 통계적 추론(신뢰구간과 가설 검정) 및 분산분석 등에 활용된다.